Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?
On s’intéresse à la définition de modèles stochastiques pour décrire les mouvements à grande échelle d’écoulements fluides géophysique.
En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
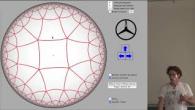
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...
Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.
Grothendieck a introduit ses fameuses topologies car sur les variétés algébriques les ouverts de Zariski sont trop peu
Nous décrivons les opérateurs différentiels tordus sur la droite projective complexe associés à un caractère entier.
Comme tous les textes affichés par un ordinateur, les lettres qui composent ce résumé sont tracées à l'aide de courbes polynomiales, les fameuses courbes de Bézier. Comment sont-elles définies ? Pourquoi sont-elles si utiles ?
Un petit aperçu des ensembles infinis et de leurs propriétés surprenantes
La longue histoire de la naissance du logarithme résumée en cinq minutes...
Sur une sphère, la somme des angles d'un triangle est reliée à son aire.
Le théorème de Mazur-Ulam établit un lien entre la structure métrique et la structure affine d'un espace vectoriel normé.
Jouer avec les nombres ou avec les figures géométriques.
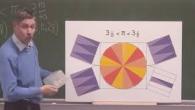
On illustre géométriquement des formules bien connues de sommes d'entiers.
Quelques chercheurs rennais tentent de répondre à cette question.
Découverte et différenciation des trois grandes géométries en dimension 2.
Parmi toutes les formes de périmètre fixé, quelle est celle qui a la plus grande surface ?