
J'essaierai de vous convaincre en 5 minutes qu'il n'est pas totalement farfelu d'appeler "droite" un tripode dans le plan.

J'essaierai de vous convaincre en 5 minutes qu'il n'est pas totalement farfelu d'appeler "droite" un tripode dans le plan.
Dans cet exposé, nous verrons que l'égalité a+b=c recèle (encore) bien des mystères et que le parallèle entre nombres et polynômes est toujours féc

Le modèle SIR est probablement le plus connu des modèles compartimentaux en épidémiologie.
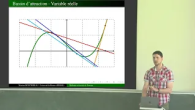
La méthode de Newton, mise au point il y a plusieurs siècles, est incontournable lorsque l'on veut approcher le zéro d'une fonction.

Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Petite introduction mathématique à la théorie de la relativité restreinte ainsi qu'à certaines de ses conséquences (contraction des longueurs, "par

On va expliquer pourquoi les électrons (de charge électrique négative) ne s'effondrent pas sur les noyaux (de charge électrique positive).

Quels polygones permettent de paver le plan ? La classification des polygones qui peuvent paver le plan s'est achevé en 2017 (enfin, on l'espère).
Toute communication sur un canal de propagation (radio, fibre optique, etc.) est susceptible d'être perturbée, ce qui peut conduire à des erreurs

Avec pour motivation l'étude de l'équidécomposabilité des polyèdres, nous discutons la rationalité d'une famille de rapports d'angles.

Les courbes elliptiques et leur utilisation pour la signature électronique.

Théorème de réciprocité quadratique : si belle et si mystérieuse.

La compression efficace des données (notamment image et audio) est un sujet de plus en plus important depuis l’ère d’internet.

Considérons une population et un ensemble d’individus choisis au hasard dans cette population.

On présente une bijection entre certains diagrammes de Young et des chemins de Dyck ...

Le Théorème de Jordan-Schoenflies nous dit qu’une courbe fermée simple du plan peut être envoyée sur un cercle standard via ...

Qu'est-ce qu'une Équation Différentielle Stochastique ?
Qui a eu l'idée de rajouter un mouvement brownien ...

Depuis le XIXe siècle, on sait qu'il existe d'autres « géométries » que la géométrie euclidienne que l'on apprend habituellement à l'école.

Le théorème d'incomplétude énonce [...] que toute théorie mathématique, assez puissante pour formuler l'arithmétique en son sein, n'est pas complète.

Dans une salle tapissée de miroirs balayée par un rayon laser, peut-il y avoir des endroits sombres ? ...
Il n'existe pas d'algorithme qui, sur présentation d'une équation polynomiale à coefficients entiers...

Poursuivons la discussion sur les solitons initiée il y a 4 ans à l'aide d'un système dynamique discret dénommé box-ball...

La physique quantique est une théorie intrinsèquement et irréductiblement aléatoire ...

Si on s’amuse à lancer une bille vers une autre bille immobile...

Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...

Dans la tradition musicale occidentale, nous nous sommes habitués à écouter des instruments qui sont accordés de manière fausse...

En 1637, Descartes appelle courbes géométriques celles que l’on peut décrire par des mouvements bien réglés...

Grâce à leurs propriétés mécaniques particulières, [...] les élastomères sont de plus en plus employés dans de nombreux domaines industriels, notamment l’étanchéité.