
En 1926, trois mathématiciens déjeunent ensemble.

En 1926, trois mathématiciens déjeunent ensemble.

La théorie spectrale fournit un outil très puissant pour l’étude des fonctions de matrices hermitiennes.

Le terme "blow up" recouvre plusieurs cadres en mathématiques (mais pas uniquement).

L’objectif est de se pencher 5 minutes sur les motivations de l’analyse sur les groupes de Lie dans l’esprit des travaux d’Élias Stein (1931-2018)

On raconte l'histoire mathématique de la forme optimale de la double bulle de savon.

En 1905, Henri Lebesgue énonce le lemme bien utile, mais faux (!), que la projection d'un ensemble Borel mesurable du plan sur la droite est encore
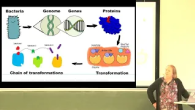
La biologie moléculaire est un exemple de domaine qui force régulièrement les chercheurs à revisiter des concepts pour répondre à des questions a p

En 1978, Murray S.Klamkin a posé la question suivante dans Mathematics Magazine : existe-t-il un nombre premier tel que si n'importe lequel de ses
Dans cet exposé, nous verrons que l'égalité a+b=c recèle (encore) bien des mystères et que le parallèle entre nombres et polynômes est toujours féc

Le modèle SIR est probablement le plus connu des modèles compartimentaux en épidémiologie.

Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Petite introduction mathématique à la théorie de la relativité restreinte ainsi qu'à certaines de ses conséquences (contraction des longueurs, "par

On va expliquer pourquoi les électrons (de charge électrique négative) ne s'effondrent pas sur les noyaux (de charge électrique positive).
Toute communication sur un canal de propagation (radio, fibre optique, etc.) est susceptible d'être perturbée, ce qui peut conduire à des erreurs &

Théorème de réciprocité quadratique : si belle et si mystérieuse.

La compression efficace des données (notamment image et audio) est un sujet de plus en plus important depuis l’ère d’internet.

Considérons une population et un ensemble d’individus choisis au hasard dans cette population.

On présente une bijection entre certains diagrammes de Young et des chemins de Dyck ...

Le Théorème de Jordan-Schoenflies nous dit qu’une courbe fermée simple du plan peut être envoyée sur un cercle standard via ...

Qu'est-ce qu'une Équation Différentielle Stochastique ?
Qui a eu l'idée de rajouter un mouvement brownien ...

Le théorème d'incomplétude énonce [...] que toute théorie mathématique, assez puissante pour formuler l'arithmétique en son sein, n'est pas complète.
Il n'existe pas d'algorithme qui, sur présentation d'une équation polynomiale à coefficients entiers...

Poursuivons la discussion sur les solitons initiée il y a 4 ans à l'aide d'un système dynamique discret dénommé box-ball...

La physique quantique est une théorie intrinsèquement et irréductiblement aléatoire ...

Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...

Grâce à leurs propriétés mécaniques particulières, [...] les élastomères sont de plus en plus employés dans de nombreux domaines industriels, notamment l’étanchéité.

Quand on dessine le théorème d’Ostrowski, on obtient un espace de Berkovich : cela permet de considérer un entier relatif comme une fonction continue sur un arbre.

Le jeu du prisonnier, ou comment s'échapper d'un domaine du plan le plus efficacement possible à l'aide de la courbure moyenne.
On décrira l'équation de la chaînette sous sa forme architecturale.

« Il suffit de faire deux fois le tour du trou pour qu'il disparaisse ! ». Nous donnerons un sens à ce phénomène et en ferons une illustration concrète.