
Depuis le XIXe siècle, on sait qu'il existe d'autres « géométries » que la géométrie euclidienne que l'on apprend habituellement à l'école.

Depuis le XIXe siècle, on sait qu'il existe d'autres « géométries » que la géométrie euclidienne que l'on apprend habituellement à l'école.

Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?

On s’intéresse à la définition de modèles stochastiques pour décrire les mouvements à grande échelle d’écoulements fluides géophysique.

En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
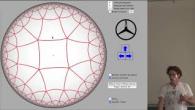
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...

Dans une salle tapissée de miroirs balayée par un rayon laser, peut-il y avoir des endroits sombres ? ...
Il n'existe pas d'algorithme qui, sur présentation d'une équation polynomiale à coefficients entiers...

La physique quantique est une théorie intrinsèquement et irréductiblement aléatoire ...

Si on s’amuse à lancer une bille vers une autre bille immobile...

Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...

Dans la tradition musicale occidentale, nous nous sommes habitués à écouter des instruments qui sont accordés de manière fausse...
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...

Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.

Une des manières les plus naturelles de ranger 8 boules de pétanque et un cochonnet dans une pochette cubique ...

Comment marier un groupe de garçons et de filles en tenant compte de leurs préférences ?.

Comme tous les textes affichés par un ordinateur, les lettres qui composent ce résumé sont tracées à l'aide de courbes polynomiales, les fameuses courbes de Bézier. Comment sont-elles définies ? Pourquoi sont-elles si utiles ?

Quelles formes doit avoir un verre pour qu'un faisceau lumineux issu d'un point, qui le transverse, converge en un point

Histoire de l'apparition de la perspective dans la peinture.

Que disent exactement la construction des entiers de Von Neumann et les résultats sur l'hypothèse du continu ?

Un petit aperçu des ensembles infinis et de leurs propriétés surprenantes
Comment, par des expériences locales, deviner la forme d'un espace ? On se laissera guider par Henri Poincaré.

Sur une sphère, la somme des angles d'un triangle est reliée à son aire.

Le théorème de Mazur-Ulam établit un lien entre la structure métrique et la structure affine d'un espace vectoriel normé.

Nous expliquerons comment un résultat de topologie peut être utilisé à des fins criminelles.

Une enquête policière fictive qui nous mène vers la théorie des graphes.

Une énigme mathématique basée sur de la combinatoire des permutations.