Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?
En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
Un joueur est placé devant trois portes fermées. Derrière l'une d'elles se trouve une voiture...
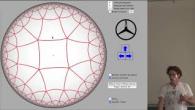
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...
Nous évoquerons en trois dates (1921, 1953, 1965) et trois noms...
Les méthodes de discrétisation des EDP ont été développées au siècle dernier...
Nous parlerons de certains risques qui peuvent survenir lorsqu’on joue au casino.
les suites de Goodstein forment un exemple 'simple' d'algorithme récursif arithmétique...
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...
Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.
Comment marier un groupe de garçons et de filles en tenant compte de leurs préférences ?.
Comme tous les textes affichés par un ordinateur, les lettres qui composent ce résumé sont tracées à l'aide de courbes polynomiales, les fameuses courbes de Bézier. Comment sont-elles définies ? Pourquoi sont-elles si utiles ?
Comment reconnaître les situations de proportionnalité à l'aide de parallélogrammes
La longue histoire de la naissance du logarithme résumée en cinq minutes...
Comment utiliser la théorie de tresses pour mélanger au mieux de fluides.
Ou comment dupliquer des lingots d'or.
Un peu de combinatoire autour d'un problème qui nous touche lors d'un grand voyage en train.
Sur une sphère, la somme des angles d'un triangle est reliée à son aire.
Jouer avec les nombres ou avec les figures géométriques.
On illustre géométriquement des formules bien connues de sommes d'entiers.
Une enquête policière fictive qui nous mène vers la théorie des graphes.
Quelques chercheurs rennais tentent de répondre à cette question.
Découverte et différenciation des trois grandes géométries en dimension 2.
L'analogie entre entier et polynôme a donné naissance à une correspondance entre arithmétique et géométrie.
Parmi toutes les formes de périmètre fixé, quelle est celle qui a la plus grande surface ?