
Nous expliquons mathématiquement le mouvement d'un électron dans un champ magnétique non uniforme.

Nous expliquons mathématiquement le mouvement d'un électron dans un champ magnétique non uniforme.

Le triangle de Penrose est un objet imaginaire qu'on peut dessiner mais pas construire en 3D.
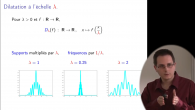
Que souhaite-t-on mesurer ? Amplitude, support, fréquence ? Comment le quantifier ?
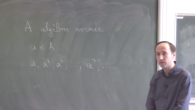
On aborde quelques aspects de l'étude des suites géométriques dans des algèbres de Banach

Jouer avec les nombres ou avec les figures géométriques.

On illustre géométriquement des formules bien connues de sommes d'entiers.

Quelle est donc cette mystérieuse courbe qui permet à Huygens en 1657 de construire des horloges à balancier très préc

Lorsqu'on cherche à inverser la courbe du chômage, on se contente parfois d'une croissance moins rapide...

Le théorème de Lagrange énonce que l’ordre d’un sous-groupe d’un groupe fini divise l’ordre de ce groupe...

Nous proposons une petite introduction à la mécanique quantique en étudiant d'abord le modèle classique du ressort.

Platon attribue à Théodore de Cyrène la preuve de l’irrationalité des racines de 3, 5, 6, 7, 8, 10, 11, 12, 13, 14 15 et 17.

Quelques chercheurs rennais tentent de répondre à cette question.

Quelles sommes peut-on obtenir lorsque l'on s'autorise à modifier l'ordre des termes dans une série ?

L'algorithme qui a permis la détection des ondes gravitationnelles utilise des travaux mathématiques sur les analyses temps-fréquence

L'analogie entre entier et polynôme a donné naissance à une correspondance entre arithmétique et géométrie.

L'ensemble des matrices symétriques réelles définies est un exemple typique de cône homogène...

Un oscillateur seul, ça oscille. Deux oscillateurs couplés, ça oscille encore mais pas n'importe comment surtout si ça résonne !

Jusqu'où peut-on faire pencher une tour de cartes sans qu’elle ne tombe ?

Comment se comporte un « grand » objet combinatoire ? Comment paver un grand diamant aztèque par des dominos ?

La mal nommée décomposition de Dunford est une décomposition d'une application linéaire en somme d'une application diagonalisable et d'une application nilpotente...

Les nombres p-adiques sont des nombres qui, contrairement aux nombres usuels, possèdent une infinité de chiffres avant la virgule...

Partant d'une identité différentielle dont on peut saisir le sens en L1, on évoquera plusieurs preuves possibles...

Qu'est-ce qui pousse un ingénieur Écossais à lancer son cheval au galop le long d'un canal ?