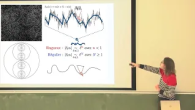
On met en branle un fluide en créant un grand tourbillon qui redistribue l'énergie qu'il a reçu à de plus petits tourbillons et ainsi de suite.

On met en branle un fluide en créant un grand tourbillon qui redistribue l'énergie qu'il a reçu à de plus petits tourbillons et ainsi de suite.

On dénombre des démonstrations du théorème de d'Alembert-Gauss de toute nature.

Cet exposé sera l'occasion de montrer comment les outils de développement informatique contribuent à améliorer la reproductibilité en science et co

Quand on mélange un Rubik's cube, on fait des mouvements au hasard pendant un certain temps.
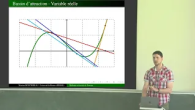
La méthode de Newton, mise au point il y a plusieurs siècles, est incontournable lorsque l'on veut approcher le zéro d'une fonction.

J'ai choisi de vous présenter ma résidence artistique au travers des deux projets que je mène conjointement.
Qui n’a jamais rêvé de faire de l’analyse sur le corps des nombres p-adiques ?
En 1902, Burnside pose la question suivante "Un groupe de type fini de torsion est-il nécessairement fini ?".

Divers travaux de recherche ont montré que, sans en avoir conscience, les enseignant-es peuvent contribuer à renforcer des inégalités entre les sex

Née dans les années 70, puis largement popularisée dans la communauté physicienne au cours des années 80/90, la théorie de la décohérence est possi

D'où viennent les statistiques ? À quoi et à qui servent-elles ? Avons-nous raison de penser qu'on peut "faire tout dire aux chiffres" ?

L'année 2022 a vu émerger la question des mathématiques au lycée dans le débat public au travers des médias et de la campagne présidentielle.

Quels polygones permettent de paver le plan ? La classification des polygones qui peuvent paver le plan s'est achevé en 2017 (enfin, on l'espère).

Considérons le polynôme f(z)=z^2. Le point z=0 est un point fixe attractif.

Avec pour motivation l'étude de l'équidécomposabilité des polyèdres, nous discutons la rationalité d'une famille de rapports d'angles.

Les courbes elliptiques et leur utilisation pour la signature électronique.

C'est l'une des questions classiques posées aux économistes : "Comment crée-t-on de la richesse économique ?".

Depuis le XIXe siècle, on sait qu'il existe d'autres « géométries » que la géométrie euclidienne que l'on apprend habituellement à l'école.

Trois épisodes de la série, Trois professeures mathématiciennes pionnières à la Faculté des sciences de Rennes en 1960 ...

Trois épisodes de la série, Trois professeures mathématiciennes pionnières à la Faculté des sciences de Rennes en 1960 ...

Trois épisodes de la série, Trois professeures mathématiciennes pionnières à la Faculté des sciences de Rennes en 1960 ...

Le Centre International de Mathématiques Pures et Appliquées est une association qui a pour but de promouvoir la recherche en mathématiques ...

Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?

En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?

Un joueur est placé devant trois portes fermées. Derrière l'une d'elles se trouve une voiture...

La menace du stéréotype est un concept de psychologie sociale expliquant par exemple certaines difficultés des filles en mathématiques. ...
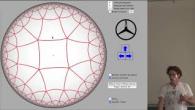
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...

La politique de la concurrence vise à encadrer le comportement des entreprises sur le marché pour y maintenir un niveau de concurrence satisfaisant. ...

Dans une salle tapissée de miroirs balayée par un rayon laser, peut-il y avoir des endroits sombres ? ...