Depuis le XIXe siècle, on sait qu'il existe d'autres « géométries » que la géométrie euclidienne que l'on apprend habituellement à l'école.
Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?
En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
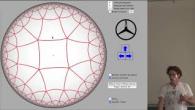
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...
Dans une salle tapissée de miroirs balayée par un rayon laser, peut-il y avoir des endroits sombres ? ...
Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...
Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.
Une des manières les plus naturelles de ranger 8 boules de pétanque et un cochonnet dans une pochette cubique ...
En 1878, Pafnouti Tchebychev présentait à l'Exposition Universelle de Paris une "machine plantigrade".