Depuis le XIXe siècle, on sait qu'il existe d'autres « géométries » que la géométrie euclidienne que l'on apprend habituellement à l'école.
Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?
En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
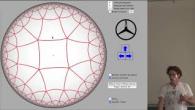
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...
Dans une salle tapissée de miroirs balayée par un rayon laser, peut-il y avoir des endroits sombres ? ...
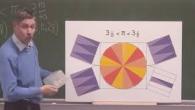
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...
En 1637, Descartes appelle courbes géométriques celles que l’on peut décrire par des mouvements bien réglés...
Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.
Une des manières les plus naturelles de ranger 8 boules de pétanque et un cochonnet dans une pochette cubique ...
fffffffff(x)=x ? Quelles périodes apparaissent lorsque nous itérons une fonction sur l’intervalle ?
En 1878, Pafnouti Tchebychev présentait à l'Exposition Universelle de Paris une "machine plantigrade".
Comme tous les textes affichés par un ordinateur, les lettres qui composent ce résumé sont tracées à l'aide de courbes polynomiales, les fameuses courbes de Bézier. Comment sont-elles définies ? Pourquoi sont-elles si utiles ?
Quelles formes doit avoir un verre pour qu'un faisceau lumineux issu d'un point, qui le transverse, converge en un point
Histoire de l'apparition de la perspective dans la peinture.
La longue histoire de la naissance du logarithme résumée en cinq minutes...
Sur une sphère, la somme des angles d'un triangle est reliée à son aire.
Le triangle de Penrose est un objet imaginaire qu'on peut dessiner mais pas construire en 3D.
Jouer avec les nombres ou avec les figures géométriques.
On illustre géométriquement des formules bien connues de sommes d'entiers.
Platon attribue à Théodore de Cyrène la preuve de l’irrationalité des racines de 3, 5, 6, 7, 8, 10, 11, 12, 13, 14 15 et 17.
Quelques chercheurs rennais tentent de répondre à cette question.
Découverte et différenciation des trois grandes géométries en dimension 2.
Parmi toutes les formes de périmètre fixé, quelle est celle qui a la plus grande surface ?
Pourquoi de bons élèves peuvent devenir des étudiants en difficulté ?
Si l’on veut construire un solide régulier de l’espace, il n’y a que 5 possibilités !
Comment reconnaître si une tresse est vraiment tressée ? Est-ce qu'un ordinateur est capable de le faire rapidement ?
Comment se comporte un « grand » objet combinatoire ? Comment paver un grand diamant aztèque par des dominos ?
Les nombres p-adiques sont des nombres qui, contrairement aux nombres usuels, possèdent une infinité de chiffres avant la virgule...