Les lois de conservation sont des principes fondamentaux en physique (conservation de l'énergie, conservation de la quantité de mouvement, etc).

La méthode d'Euler, intégrateur numérique central dans l'approximation de solutions d'équations différentielles, fait raisonnablement bien son job.

Les modèles de diffusion sont actuellement l'état de l'art des modèles génératifs développés en apprentissage automatique.

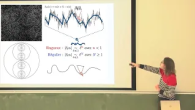
On met en branle un fluide en créant un grand tourbillon qui redistribue l'énergie qu'il a reçu à de plus petits tourbillons et ainsi de suite.

On dénombre des démonstrations du théorème de d'Alembert-Gauss de toute nature.

Quand on mélange un Rubik's cube, on fait des mouvements au hasard pendant un certain temps.

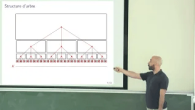
Qui n’a jamais rêvé de faire de l’analyse sur le corps des nombres p-adiques ?

En 1902, Burnside pose la question suivante "Un groupe de type fini de torsion est-il nécessairement fini ?".

Née dans les années 70, puis largement popularisée dans la communauté physicienne a

Considérons le polynôme f(z)=z^2. Le point z=0 est un point fixe attractif.