
Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Depuis le XIXe siècle, on sait qu'il existe d'autres « géométries » que la géométrie euclidienne que l'on apprend habituellement à l'école.

Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?

Le théorème d'incomplétude énonce [...] que toute théorie mathématique, assez puissante pour formuler l'arithmétique en son sein, n'est pas complète.

En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
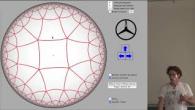
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...

Dans une salle tapissée de miroirs balayée par un rayon laser, peut-il y avoir des endroits sombres ? ...

Nous évoquerons en trois dates (1921, 1953, 1965) et trois noms...

Les méthodes de discrétisation des EDP ont été développées au siècle dernier...

les suites de Goodstein forment un exemple 'simple' d'algorithme récursif arithmétique...

Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...

En 1637, Descartes appelle courbes géométriques celles que l’on peut décrire par des mouvements bien réglés...

Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.

Une des manières les plus naturelles de ranger 8 boules de pétanque et un cochonnet dans une pochette cubique ...

En 1878, Pafnouti Tchebychev présentait à l'Exposition Universelle de Paris une "machine plantigrade".

Grothendieck a introduit ses fameuses topologies car sur les variétés algébriques les ouverts de Zariski sont trop peu

Nous décrivons les opérateurs différentiels tordus sur la droite projective complexe associés à un caractère entier.

Comme tous les textes affichés par un ordinateur, les lettres qui composent ce résumé sont tracées à l'aide de courbes polynomiales, les fameuses courbes de Bézier. Comment sont-elles définies ? Pourquoi sont-elles si utiles ?

Quand on dessine le théorème d’Ostrowski, on obtient un espace de Berkovich : cela permet de considérer un entier relatif comme une fonction continue sur un arbre.

Quelles formes doit avoir un verre pour qu'un faisceau lumineux issu d'un point, qui le transverse, converge en un point

Histoire de l'apparition de la perspective dans la peinture.

« Il suffit de faire deux fois le tour du trou pour qu'il disparaisse ! ». Nous donnerons un sens à ce phénomène et en ferons une illustration concrète.

Que dire de l'équation de Fermat lorsqu'on cherche ses solutions modulo un nombre premier ?

La longue histoire de la naissance du logarithme résumée en cinq minutes...
Comment utiliser la théorie de tresses pour mélanger au mieux de fluides.
Ou comment dupliquer des lingots d'or.

Nous expliquons ce qu'est le problème du logarithme discret sur lequel repose la sécurité de la plupart des crypto-systèmes à clef publique.

Sur une sphère, la somme des angles d'un triangle est reliée à son aire.