
Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Qu'est-ce qu'une Équation Différentielle Stochastique ?
Qui a eu l'idée de rajouter un mouvement brownien ...

Le théorème d'incomplétude énonce [...] que toute théorie mathématique, assez puissante pour formuler l'arithmétique en son sein, n'est pas complète.

Nous évoquerons en trois dates (1921, 1953, 1965) et trois noms...

Les méthodes de discrétisation des EDP ont été développées au siècle dernier...

les suites de Goodstein forment un exemple 'simple' d'algorithme récursif arithmétique...

Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...

Quand on dessine le théorème d’Ostrowski, on obtient un espace de Berkovich : cela permet de considérer un entier relatif comme une fonction continue sur un arbre.

« Il suffit de faire deux fois le tour du trou pour qu'il disparaisse ! ». Nous donnerons un sens à ce phénomène et en ferons une illustration concrète.

Que dire de l'équation de Fermat lorsqu'on cherche ses solutions modulo un nombre premier ?
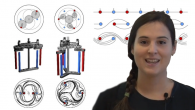
Comment utiliser la théorie de tresses pour mélanger au mieux de fluides.
Ou comment dupliquer des lingots d'or.

Nous expliquons ce qu'est le problème du logarithme discret sur lequel repose la sécurité de la plupart des crypto-systèmes à clef publique.

Le théorème de Lagrange énonce que l’ordre d’un sous-groupe d’un groupe fini divise l’ordre de ce groupe...

De la physique statistique et des rebonds des balles de billards aux mathématiques.

L'analogie entre entier et polynôme a donné naissance à une correspondance entre arithmétique et géométrie.

La mal nommée décomposition de Dunford est une décomposition d'une application linéaire en somme d'une application diagonalisable et d'une application nilpotente...

On fait tomber des allumettes sur un parquet dont les lattes sont régulièrement espacées...