
Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.

Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?

Le théorème d'incomplétude énonce [...] que toute théorie mathématique, assez puissante pour formuler l'arithmétique en son sein, n'est pas complète.

En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
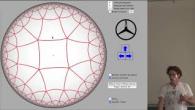
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...

Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...
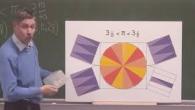
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...

Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.

Comme tous les textes affichés par un ordinateur, les lettres qui composent ce résumé sont tracées à l'aide de courbes polynomiales, les fameuses courbes de Bézier. Comment sont-elles définies ? Pourquoi sont-elles si utiles ?

Quand on dessine le théorème d’Ostrowski, on obtient un espace de Berkovich : cela permet de considérer un entier relatif comme une fonction continue sur un arbre.

« Il suffit de faire deux fois le tour du trou pour qu'il disparaisse ! ». Nous donnerons un sens à ce phénomène et en ferons une illustration concrète.

Que dire de l'équation de Fermat lorsqu'on cherche ses solutions modulo un nombre premier ?

La longue histoire de la naissance du logarithme résumée en cinq minutes...

Nous expliquons ce qu'est le problème du logarithme discret sur lequel repose la sécurité de la plupart des crypto-systèmes à clef publique.

Sur une sphère, la somme des angles d'un triangle est reliée à son aire.

Jouer avec les nombres ou avec les figures géométriques.

On illustre géométriquement des formules bien connues de sommes d'entiers.

Le théorème de Lagrange énonce que l’ordre d’un sous-groupe d’un groupe fini divise l’ordre de ce groupe...

Quelques chercheurs rennais tentent de répondre à cette question.

Découverte et différenciation des trois grandes géométries en dimension 2.

Parmi toutes les formes de périmètre fixé, quelle est celle qui a la plus grande surface ?

La mal nommée décomposition de Dunford est une décomposition d'une application linéaire en somme d'une application diagonalisable et d'une application nilpotente...