Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.
Le théorème d'incomplétude énonce [...] que toute théorie mathématique, assez puissante pour formuler l'arithmétique en son sein, n'est pas complète.
Poursuivons la discussion sur les solitons initiée il y a 4 ans à l'aide d'un système dynamique discret dénommé box-ball...
En 1637, Descartes appelle courbes géométriques celles que l’on peut décrire par des mouvements bien réglés...
Grâce à leurs propriétés mécaniques particulières, [...] les élastomères sont de plus en plus employés dans de nombreux domaines industriels, notamment l’étanchéité.
En 1878, Pafnouti Tchebychev présentait à l'Exposition Universelle de Paris une "machine plantigrade".
Dans les écoulements rapides ou de grande taille, comme les courants océaniques, les prévisions déterministes sont ent
Après le 21 décembre, les jours rallongent. Pourtant, ils continuent de diminuer le matin jusque début janvier...
Quand on dessine le théorème d’Ostrowski, on obtient un espace de Berkovich : cela permet de considérer un entier relatif comme une fonction continue sur un arbre.
Le jeu du prisonnier, ou comment s'échapper d'un domaine du plan le plus efficacement possible à l'aide de la courbure moyenne.
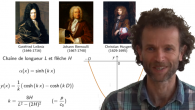
On décrira l'équation de la chaînette sous sa forme architecturale.
« Il suffit de faire deux fois le tour du trou pour qu'il disparaisse ! ». Nous donnerons un sens à ce phénomène et en ferons une illustration concrète.
Que dire de l'équation de Fermat lorsqu'on cherche ses solutions modulo un nombre premier ?
Où l'on présente la méthode d'Euler et quelques raffinements pour calculer des solutions approchées d'équations différentielles.
Nous expliquons ce qu'est le problème du logarithme discret sur lequel repose la sécurité de la plupart des crypto-systèmes à clef publique.
Où l'on explique comment extraire de l'énergie des trous-noirs pour fabriquer des centrales ou des bombes...
La simulation du système solaire est un problème académique qui permet l'analyse du comportement des méthodes numériques.
Nous expliquons mathématiquement le mouvement d'un électron dans un champ magnétique non uniforme.
Le triangle de Penrose est un objet imaginaire qu'on peut dessiner mais pas construire en 3D.
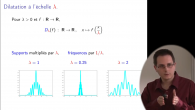
Que souhaite-t-on mesurer ? Amplitude, support, fréquence ? Comment le quantifier ?
Quelle est donc cette mystérieuse courbe qui permet à Huygens en 1657 de construire des horloges à balancier très préc
Lorsqu'on cherche à inverser la courbe du chômage, on se contente parfois d'une croissance moins rapide...
Le théorème de Lagrange énonce que l’ordre d’un sous-groupe d’un groupe fini divise l’ordre de ce groupe...
Nous proposons une petite introduction à la mécanique quantique en étudiant d'abord le modèle classique du ressort.
Platon attribue à Théodore de Cyrène la preuve de l’irrationalité des racines de 3, 5, 6, 7, 8, 10, 11, 12, 13, 14 15 et 17.
L'algorithme qui a permis la détection des ondes gravitationnelles utilise des travaux mathématiques sur les analyses temps-fréquence
Un oscillateur seul, ça oscille. Deux oscillateurs couplés, ça oscille encore mais pas n'importe comment surtout si ça résonne !
Où l'on découvre l'histoire des différentes modélisations et représentations du champ de contrainte dans un milieu continu.
Comment se comporte un « grand » objet combinatoire ? Comment paver un grand diamant aztèque par des dominos ?