Qu'est-ce qu'une Équation Différentielle Stochastique ?
Qui a eu l'idée de rajouter un mouvement brownien ...
Pourquoi, à l'ère du numérique, la quadrature du cercle n'est pas si inextricable qu'elle le fut ?
En 1917 Kakeya pose à la communauté mathématique la question suivante : Qu'elle est la surface d'aire minimale à l'intérieur de laquelle il est possible de retourner entièrement une aiguille ?
Un joueur est placé devant trois portes fermées. Derrière l'une d'elles se trouve une voiture...
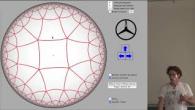
le plan hyperbolique est un exemple très important de géométrie non-euclidienne. On va se promener dans cet espace ...
La politique de la concurrence vise à encadrer le comportement des entreprises sur le marché pour y maintenir un niveau de concurrence satisfaisant. ...
Nous parlerons de certains risques qui peuvent survenir lorsqu’on joue au casino.
Le problème des nombres congruents consiste à montrer qu’un entier donné est l’aire d’un triangle rectangle à côtés rationnels...
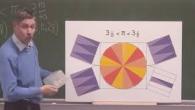
Après avoir rappelé les résultats de l'Antiquité sur le cercle ...
Le théorème de Jordan [...] est un exemple remarquable d'énoncé intuitivement vrai.
Comme tous les textes affichés par un ordinateur, les lettres qui composent ce résumé sont tracées à l'aide de courbes polynomiales, les fameuses courbes de Bézier. Comment sont-elles définies ? Pourquoi sont-elles si utiles ?
Le jeu du prisonnier, ou comment s'échapper d'un domaine du plan le plus efficacement possible à l'aide de la courbure moyenne.
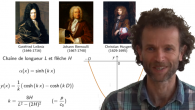
On décrira l'équation de la chaînette sous sa forme architecturale.
Comment reconnaître les situations de proportionnalité à l'aide de parallélogrammes
L'équation de Navier-Stokes, dont la résolution est mise à prix, modélise le mouvement des fluides visqueux.
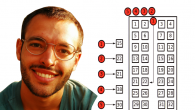
Un peu de combinatoire autour d'un problème qui nous touche lors d'un grand voyage en train.
La simulation du système solaire est un problème académique qui permet l'analyse du comportement des méthodes numériques.
Nous expliquons mathématiquement le mouvement d'un électron dans un champ magnétique non uniforme.
Sur une sphère, la somme des angles d'un triangle est reliée à son aire.
Le théorème de Mazur-Ulam établit un lien entre la structure métrique et la structure affine d'un espace vectoriel normé.
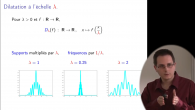
Que souhaite-t-on mesurer ? Amplitude, support, fréquence ? Comment le quantifier ?
Nous proposons une petite introduction à la mécanique quantique en étudiant d'abord le modèle classique du ressort.
Quelles sommes peut-on obtenir lorsque l'on s'autorise à modifier l'ordre des termes dans une série ?
De la physique statistique et des rebonds des balles de billards aux mathématiques.
Découverte et différenciation des trois grandes géométries en dimension 2.
Parmi toutes les formes de périmètre fixé, quelle est celle qui a la plus grande surface ?
Jusqu'où peut-on faire pencher une tour de cartes sans qu’elle ne tombe ?
Partant d'une identité différentielle dont on peut saisir le sens en L1, on évoquera plusieurs preuves possibles...