À venir
Minicourses
Tsachik Gelander (Weizmann Institute)
$\mathrm{Aut}(\mathrm{F}_n)$ actions on deformation varieties.François Labourie (Université de Nice-Sophia Antipolis)
Surface subgroups in higher rank lattices.Julien Marché (Université Pierre et Marie Curie)
Dynamics on character varieties of surface groups into $\mathrm{SU}_2$ and $\mathrm{SL}_2(\mathbb{R})$.Research talks
Sam Ballas (UCSB - Florida St.)
Generalized cusps in convex projective manifolds.Juliette Bavard (University of Chicago)
Around a big mapping class group.Ken Bromberg (University of Utah)
The gradient flow of renormalized volume.Federica Fanoni (Max Plank)
Basmajian-type inequalities for maximal representations.Fanny Kassel (I.H.E.S)
Convex cocompactness in real projective geometry.Gye-Seon Lee (Heidelberg)
Convex real projective Dehn fillings.Gabriele Mondello (Sapienza, Università di Roma)
On the topology the representation variety of a punctured surface group in $\mathrm{PSL}(2,\mathbb{R})$.Maria Beatrice Pozzetti (University of Heildelberg)
Laminations for some limits of maximal representations.Andres Sambarino (Université Pierre et Marie Curie)
Liouville current, intersection and pressure metric revisited.Nicolas Tholozan (ENS Paris)
Compact components of relative character varieties.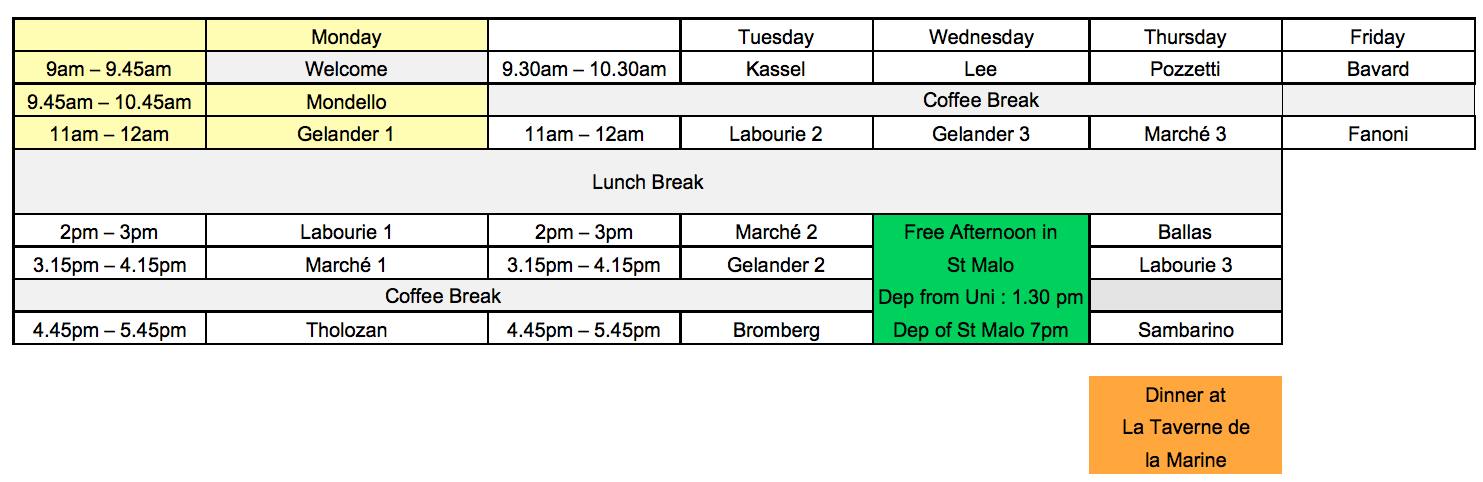 Abstracts:
Abstracts:
Tsachik Gelander, $\mathrm{Aut}(\mathrm{F}_n)$ actions on deformation varieties.
For a group $G$ and an integer $n$, consider the deformation space $X=\mathrm{Hom}(\mathrm{F}_n,G)$. The group $\mathrm{Aut}(\mathrm{F}_n)$ acts on $X$ by pre-compositions. If $G$ carries an additional structure, e.g. if $G$ is finite, topological, measurable, differentiable or algebraic, etc. this structure is often inherited by $X$ and preserved by the action of $\mathrm{Aut}(\mathrm{F}_n)$. For instance if $G$ is a locally compact unimodular group, the Haar measure on $G$ induces an $\mathrm{Aut}(\mathrm{F}_n)$-invariant measure on $X$. Analysing the action of $\mathrm{Aut}(\mathrm{F}_n)$ on $X$ is interesting both from the point of view of $G$ and of $\mathrm{Aut}(\mathrm{F}_n)$, and may contribute to the understanding of both. The course will wonder around this problem focusing on the dynamical and algebro geometric aspects of it.François Labourie, Surface subgroups in higher rank lattices.
In this mini course, I will survey a construction of surfaces subgroups in lattices of a semi simple subgroup G. I will focus for the sake of simplicity on the case $\mathrm{G}= \mathrm{SL}(n,\mathbb{C})$. This is a joint work with Jeremy Kahn and Shahar Mozes.Julien Marché, Dynamics on character varieties of surface groups into $\mathrm{SU}_2$ and $\mathrm{SL}_2(\mathbb{R})$.
We will study the algebraic and symplectic geometry of these character varieties and prove the ergodicity of the action of the mapping class group on these spaces when it is known. ⛤ ⛤ ⛤Sam Ballas, Generalized cusps in convex projective manifolds.
A generalized cusp is a generalization of a cusp of a finite volume hyperbolic manifold. In this talk I will discuss the geometry of these cusps, how they can be classified, and interesting transitional properties related to non-Hausdorff behavior of the moduli space of generalized cusps. This is joint work with Daryl Cooper and Arielle Leitner.Juliette Bavard, Around a big mapping class group.
In this talk, I will speak about the mapping class group of the plane minus a Cantor set. After recalling several dynamical contexts in which this group naturally appears, including group actions on surfaces and complex dynamics, I will present the 'ray graph', which is a Gromov-hyperbolic graph on which this big mapping class group acts by isometries. If time allows, I will give a description of the Gromov-boundary of the ray graph in terms of long rays in the plane minus a Cantor set. This involves joint work with Alden Walker, and work in progress with Danny Calegari, Yan Mary He, Sarah Koch and Alden Walker.Ken Bromberg, The gradient flow of renormalized volume.
Renormalized volume is a way of assigning a finite volume to an convex co-compact hyperbolic $3$-manifold whose usual volume is infinite. On the space of all convex co-compact structures the renormalized volume is a smooth function whose derivative has been calculated by Krasnov-Schlenker. We will discuss the gradient flow of renormalized volume and show how studying this flow leads to implications on the geometry of the manifolds. This is joint work with M. Bridgeman and J. Brock.Federica Fanoni, Basmajian-type inequalities for maximal representations.
Basmajian's celebrated identity gives a way to compute the length of the boundary of a hyperbolic surface in terms of the lengths of the so-called orthogeodesics (geodesics orthogonal to the boundary at both endpoints). This identity can be generalized to the context of maximal representations. This is a class of representations of the fundamental group of a surface that can be seen as a generalization of Teichmüller space. I will describe the classical identity, introduce maximal representations and discuss Basmajian's identity in this setup. Joint work with Beatrice Pozzetti.Fanny Kassel, Convex cocompactness in real projective geometry.
We will discuss a notion of convex cocompactness for discrete groups preserving a properly convex open domain in real projective space. For hyperbolic groups, this notion is equivalent to being the image of a projective Anosov representation. For nonhyperbolic groups, the notion covers Benoist's examples of divisible convex sets which are not strictly convex, as well as their deformations inside larger projective spaces. Even when these groups are nonhyperbolic, they still share some of the good properties of classical convex cocompact subgroups of rank-one Lie groups; in particular, they are quasi-isometrically embedded and structurally stable. This is joint work with J. Danciger and F. Guéritaud.Gye-Seon Lee, Convex real projective Dehn fillings.
Thurston's hyperbolic Dehn surgery theorem says that if M is a cusped hyperbolic three dimensional manifold then almost all Dehn fillings of M admit a hyperbolic structure. However, the hyperbolic Dehn filling is impossible for dimension bigger than three. In this talk, I will give the first examples of cusped hyperbolic four dimensional manifolds whose Dehn fillings admit a convex real projective structure. Joint work with Suhyoung Choi and Ludovic Marquis.Gabriele Mondello, On the topology the representation variety of a punctured surface group in $\mathrm{PSL}(2,\mathbb{R})$
Goldman classified the connected components of the representation space of a closed surface group in $\mathrm{PSL}(2,\mathbb{R})$ and Hitchin described the topology of the components with nonzero Euler number. In this talk I will describe how to perform a similar analysis for surfaces of finite type, thus detecting the topology of the space of representations of a punctured surface in $\mathrm{PSL}(2,\mathbb{R})$ with constrained peripheral values and nonzero Euler number. I follow Hitchin's strategy and I exploit Simpson's correspondence between representations of punctured surface groups and parabolic Higgs bundles.Maria Beatrice Pozzetti, Laminations for some limits of maximal representations .
Maximal representations are higher rank analogues of holonomies of hyperbolization, whose natural definition I'll recall at the beginning of my talk. Studying degenerations of such representations, I will find a clear distinction between phenomena already present in the boundary of the Teichm\"uller space and new flat features. In the fist case I will reconstruct a canonical lamination on the surface, and a tree embedding in the asymptotic cone of the symmetric space; for all other cases I will show that there is an uniform lower bound on the length of every element. Time permitting I will discuss several examples of new degenerations. Joint work with Burger, Iozzi and Parreau.Andres Sambarino, Liouville current, intersection and pressure metric revisited.
The purpose of the talk is to explain a construction of a Liouville current for a representation in the Hitchin component. Bonahon's intersection between two such currents can be computed. We will also explain the relation with a pressure metric. This is joint work with D. Canary, M. Bridgeman and F. Labourie.Nicolas Tholozan, Compact components of relative character varieties.
Benedetto and Goldman have shown that certain relative character varieties of the fundamental group of the four punctured sphere into $\mathrm{PSL}(2,\mathbb{R})$ contain a compact component diffeomorphic to the $2$-sphere.The first part of my talk will be devoted to the following generalization of this result : under an explicit condition on the images of the boundary curves, the relative character varieties of the fundamental group of the $n$-punctured sphere into $\mathrm{PSL}(2,\mathbb{R})$ contain a compact component symplectomorphic to the complex projective space of dimension $n-3$.
In the second part of the talk I will discuss some questions that arise when one considers the action of the mapping class group on these compact components. This is a joint work with Bertrand Deroin.
